The Materials Geometry group at Syracuse University studies how soft materials behave using tools from geometry and topology. We focus mainly on theoretical research with some simulations to uncover the universal features of material behavior, and use these insights to design new meta-materials.
Our research is funded mostly by the National Science Foundation with contributions from the Department of Defense and Syracuse University.
Recent highlights from our research
4D printing and self-folding structures
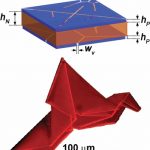
4D printing is the process of patterning a flat 2D sheet so that it dynamically folds into a complex 3D structure. This is an experimental version of a math problem, isometric embedding, which asks what shape a surface with particular properties will have. This technology enables the rapid fabrication of complex shapes at scale. The questions we want to answer are: how should flat structures be patterned to produce the shapes we want? What are the mechanical properties of the resulting structures?
Selected work on 4D printing and self-folding structures
- J. Kim, J.A. Hanna, M. Byun, C.D. Santangelo, and R.C. Hayward, “Designing responsive buckled surfaces by halftone gel lithography,” Science 335, 1201-1205 (2012).
- N. Bende, R.C. Hayward, and C.D. Santangelo, “Nonuniform growth and topological defects in the shaping of elastic sheets,” Soft Matter 10, 6382–6386 (2014).
- J.-H. Na, J. Bae, M.C. Chiappelli, A. Evans, C.D. Santangelo, R.J. Lang, T. Hull, and R.C. Hayward, “Programming reversibly self-folding origami with micropatterned photo-crosslinkable polymer trilayers,” Adv. Mat. 27, 79–85 (2015).
Designing mechanical metamaterials
Changing the geometrical structure of a material can radically change its properties. We take advantage of this to find ways to design new materials with desired effective mechanical properties. Our goal is to uncover the universal features of this kind of design to inform the connections between geometry and mechanics, and enable the rational or computational design of new materials. This includes both static properties, such as designing tunable mechanical metamaterials whose properties change with environmental conditions, and dynamic properties, where geometry and curvature can be used to guide acoustic waves.
Selected work on mechanical meta-materials
- JC Roback, A Nagrath, S Kristipati, C.D. Santangelo, and RC Hayward, “Tuning stiffness of mechanical metamaterial unit cells via transitions to second-order rigid and pre-stressed states,” Soft Matter 21, 3890-3898 (2025).
- Sourav Roy, and C.D. Santangelo, “Curvature screening in draped mechanical metamaterial sheet,” Soft Matter 19, 8150–8156 (2023).
Geometric and topological frustration
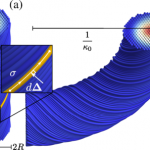
In many systems, the geometrical constraints of a material’s local structure are not compatible with global order. Think of how, for example, maps always distort the surface of the Earth no matter how they are drawn. This kind of frustration can lead to the formation of defects or control their self-assembly, and features prominently in biology from the sub-cellular scale to the organismal scale. We want to uncover the general principles behind how geometric frustration organizes structures or leads to disorder.