Manu Mannattil and Christian D. Santangelo, Phys. Rev. E 109, 035001
link to arXiv version
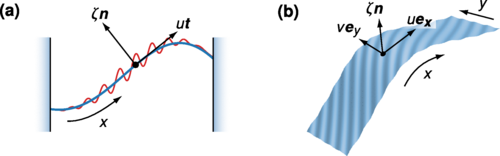
Abstract: We consider the localization of elastic waves in thin elastic structures with spatially varying curvature profiles, using a curved rod and a singly curved shell as concrete examples. Previous studies on related problems have broadly focused on the localization of flexural waves on such structures. Here, using the semiclassical WKB approximation for multicomponent waves, we show that in addition to flexural waves, extensional and shear waves also form localized, bound states around points where the absolute curvature of the structure has a minimum. We also see excellent agreement between our numerical experiments and the semiclassical results, which hinges on the vanishing of two extra phases that arise in the semiclassical quantization rule. Our findings open up novel ways to fine-tune the acoustic and vibrational properties of thin elastic structures and raise the possibility of introducing new phenomena not easily captured by effective models of flexural waves alone.